Can Regression Analysis Be Used A Data That The Distribution Is Skewed?

Set of statistical processes for estimating the relationships among variables

In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often chosen the 'outcome' or 'response' variable, or a 'characterization' in machine learning parlance) and one or more independent variables (frequently chosen 'predictors', 'covariates', 'explanatory variables' or 'features'). The most common course of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that about closely fits the information according to a specific mathematical benchmark. For example, the method of ordinary least squares computes the unique line (or hyperplane) that minimizes the sum of squared differences between the true data and that line (or hyperplane). For specific mathematical reasons (see linear regression), this allows the researcher to guess the conditional expectation (or population average value) of the dependent variable when the independent variables accept on a given set up of values. Less common forms of regression use slightly different procedures to estimate alternative location parameters (e.m., quantile regression or Necessary Condition Assay^[1]) or estimate the conditional expectation across a broader collection of non-linear models (e.k., nonparametric regression).

Regression analysis is primarily used for two conceptually distinct purposes.

Starting time, regression analysis is widely used for prediction and forecasting, where its use has substantial overlap with the field of motorcar learning.

Second, in some situations regression analysis can exist used to infer causal relationships between the contained and dependent variables. Importantly, regressions past themselves only reveal relationships between a dependent variable and a collection of contained variables in a stock-still dataset. To employ regressions for prediction or to infer causal relationships, respectively, a researcher must carefully justify why existing relationships have predictive power for a new context or why a relationship between two variables has a causal interpretation. The latter is especially important when researchers hope to gauge causal relationships using observational data.^{[ii] [3]}

History [edit]

The earliest form of regression was the method of least squares, which was published by Legendre in 1805,^[4] and past Gauss in 1809.^[five] Legendre and Gauss both applied the method to the problem of determining, from astronomical observations, the orbits of bodies well-nigh the Sunday (mostly comets, but as well later the and so newly discovered minor planets). Gauss published a farther evolution of the theory of least squares in 1821,^{[half dozen]} including a version of the Gauss–Markov theorem.

The term "regression" was coined by Francis Galton in the 19th century to describe a biological miracle. The miracle was that the heights of descendants of tall ancestors tend to backslide downwardly towards a normal average (a phenomenon too known equally regression toward the hateful).^{[7] [8]} For Galton, regression had only this biological significant,^{[9] [x]} but his work was later extended past Udny Yule and Karl Pearson to a more general statistical context.^{[11] [12]} In the work of Yule and Pearson, the articulation distribution of the response and explanatory variables is causeless to be Gaussian. This supposition was weakened past R.A. Fisher in his works of 1922 and 1925.^{[13] [14] [fifteen]} Fisher assumed that the provisional distribution of the response variable is Gaussian, merely the joint distribution demand not be. In this respect, Fisher's assumption is closer to Gauss's formulation of 1821.

In the 1950s and 1960s, economists used electromechanical desk-bound "calculators" to calculate regressions. Before 1970, it sometimes took up to 24 hours to receive the effect from ane regression.^[sixteen]

Regression methods continue to be an area of agile inquiry. In contempo decades, new methods take been developed for robust regression, regression involving correlated responses such every bit time series and growth curves, regression in which the predictor (independent variable) or response variables are curves, images, graphs, or other circuitous data objects, regression methods all-around diverse types of missing data, nonparametric regression, Bayesian methods for regression, regression in which the predictor variables are measured with mistake, regression with more predictor variables than observations, and causal inference with regression.

Regression model [edit]

In practice, researchers first select a model they would like to estimate and so use their chosen method (east.g., ordinary least squares) to gauge the parameters of that model. Regression models involve the following components:

In various fields of application, dissimilar terminologies are used in identify of dependent and independent variables.

Most regression models propose that ${\displaystyle Y_{i}}$ is a function of ${\displaystyle X_{i}}$ and ${\displaystyle \beta }$ , with ${\displaystyle e_{i}}$ representing an additive error term that may stand in for un-modeled determinants of ${\displaystyle Y_{i}}$ or random statistical noise:

${\displaystyle Y_{i}=f(X_{i},\beta )+e_{i}}$

The researchers' goal is to estimate the part ${\displaystyle f(X_{i},\beta )}$ that most closely fits the data. To carry out regression analysis, the class of the role ${\displaystyle f}$ must be specified. Sometimes the form of this role is based on knowledge about the relationship between ${\displaystyle Y_{i}}$ and ${\displaystyle X_{i}}$ that does not rely on the data. If no such cognition is available, a flexible or convenient form for ${\displaystyle f}$ is chosen. For example, a uncomplicated univariate regression may advise ${\displaystyle f(X_{i},\beta )=\beta _{0}+\beta _{1}X_{i}}$ , suggesting that the researcher believes ${\displaystyle Y_{i}=\beta _{0}+\beta _{ane}X_{i}+e_{i}}$ to be a reasonable approximation for the statistical process generating the information.

One time researchers decide their preferred statistical model, different forms of regression analysis provide tools to guess the parameters ${\displaystyle \beta }$ . For example, least squares (including its most common variant, ordinary least squares) finds the value of ${\displaystyle \beta }$ that minimizes the sum of squared errors ${\displaystyle \sum _{i}(Y_{i}-f(X_{i},\beta ))^{two}}$ . A given regression method will ultimately provide an estimate of ${\displaystyle \beta }$ , ordinarily denoted ${\displaystyle {\lid {\beta }}}$ to distinguish the estimate from the true (unknown) parameter value that generated the data. Using this guess, the researcher can then use the fitted value ${\displaystyle {\chapeau {Y_{i}}}=f(X_{i},{\hat {\beta }})}$ for prediction or to assess the accuracy of the model in explaining the data. Whether the researcher is intrinsically interested in the approximate ${\displaystyle {\hat {\beta }}}$ or the predicted value ${\displaystyle {\lid {Y_{i}}}}$ will depend on context and their goals. As described in ordinary to the lowest degree squares, to the lowest degree squares is widely used because the estimated function ${\displaystyle f(X_{i},{\hat {\beta }})}$ approximates the conditional expectation ${\displaystyle E(Y_{i}|X_{i})}$ .^[five] However, alternative variants (e.g., least absolute deviations or quantile regression) are useful when researchers want to model other functions ${\displaystyle f(X_{i},\beta )}$ .

It is important to notation that there must be sufficient information to estimate a regression model. For case, suppose that a researcher has admission to ${\displaystyle N}$ rows of data with one dependent and ii independent variables: ${\displaystyle (Y_{i},X_{1i},X_{2i})}$ . Suppose further that the researcher wants to approximate a bivariate linear model via least squares: ${\displaystyle Y_{i}=\beta _{0}+\beta _{1}X_{1i}+\beta _{2}X_{2i}+e_{i}}$ . If the researcher simply has access to ${\displaystyle Due north=2}$ data points, so they could find infinitely many combinations ${\displaystyle ({\lid {\beta }}_{0},{\hat {\beta }}_{1},{\lid {\beta }}_{two})}$ that explicate the data equally well: any combination can be chosen that satisfies ${\displaystyle {\hat {Y}}_{i}={\hat {\beta }}_{0}+{\hat {\beta }}_{1}X_{1i}+{\chapeau {\beta }}_{2}X_{2i}}$ , all of which pb to ${\displaystyle \sum _{i}{\hat {e}}_{i}^{2}=\sum _{i}({\chapeau {Y}}_{i}-({\hat {\beta }}_{0}+{\hat {\beta }}_{1}X_{1i}+{\lid {\beta }}_{two}X_{2i}))^{2}=0}$ and are therefore valid solutions that minimize the sum of squared residuals. To empathize why there are infinitely many options, note that the system of ${\displaystyle N=2}$ equations is to exist solved for 3 unknowns, which makes the system underdetermined. Alternatively, ane can visualize infinitely many 3-dimensional planes that go through ${\displaystyle Northward=2}$ fixed points.

More than generally, to estimate a to the lowest degree squares model with ${\displaystyle thousand}$ singled-out parameters, one must take ${\displaystyle N\geq k}$ singled-out information points. If ${\displaystyle Due north>yard}$ , then there does not by and large be a prepare of parameters that will perfectly fit the data. The quantity ${\displaystyle k-N}$ appears often in regression analysis, and is referred to as the degrees of freedom in the model. Moreover, to estimate a least squares model, the independent variables ${\displaystyle (X_{1i},X_{2i},...,X_{ki})}$ must exist linearly independent: one must non exist able to reconstruct any of the independent variables by adding and multiplying the remaining independent variables. Every bit discussed in ordinary to the lowest degree squares, this status ensures that ${\displaystyle X^{T}Ten}$ is an invertible matrix and therefore that a unique solution ${\displaystyle {\lid {\beta }}}$ exists.

Underlying assumptions [edit]

By itself, a regression is merely a adding using the data. In order to translate the output of regression as a meaningful statistical quantity that measures real-globe relationships, researchers often rely on a number of classical assumptions. These assumptions frequently include:

A handful of weather are sufficient for the least-squares estimator to possess desirable backdrop: in item, the Gauss–Markov assumptions imply that the parameter estimates volition be unbiased, consistent, and efficient in the class of linear unbiased estimators. Practitioners have developed a variety of methods to maintain some or all of these desirable properties in existent-world settings, considering these classical assumptions are unlikely to hold exactly. For example, modeling errors-in-variables tin lead to reasonable estimates independent variables are measured with errors. Heteroscedasticity-consistent standard errors allow the variance of ${\displaystyle e_{i}}$ to modify across values of ${\displaystyle X_{i}}$ . Correlated errors that exist within subsets of the information or follow specific patterns can exist handled using amassed standard errors, geographic weighted regression, or Newey–Westward standard errors, among other techniques. When rows of information correspond to locations in infinite, the choice of how to model ${\displaystyle e_{i}}$ within geographic units can have important consequences.^{[17] [18]} The subfield of econometrics is largely focused on developing techniques that allow researchers to make reasonable real-world conclusions in real-earth settings, where classical assumptions practise not hold exactly.

Linear regression [edit]

In linear regression, the model specification is that the dependent variable, ${\displaystyle y_{i}}$ is a linear combination of the parameters (but demand not be linear in the independent variables). For case, in simple linear regression for modeling ${\displaystyle n}$ data points at that place is i independent variable: ${\displaystyle x_{i}}$ , and two parameters, ${\displaystyle \beta _{0}}$ and ${\displaystyle \beta _{1}}$ :

directly line: ${\displaystyle y_{i}=\beta _{0}+\beta _{1}x_{i}+\varepsilon _{i},\quad i=i,\dots ,n.\!}$

In multiple linear regression, there are several independent variables or functions of independent variables.

Adding a term in ${\displaystyle x_{i}^{two}}$ to the preceding regression gives:

parabola: ${\displaystyle y_{i}=\beta _{0}+\beta _{ane}x_{i}+\beta _{2}x_{i}^{2}+\varepsilon _{i},\ i=1,\dots ,n.\!}$

This is still linear regression; although the expression on the correct manus side is quadratic in the independent variable ${\displaystyle x_{i}}$ , it is linear in the parameters ${\displaystyle \beta _{0}}$ , ${\displaystyle \beta _{ane}}$ and ${\displaystyle \beta _{2}.}$

In both cases, ${\displaystyle \varepsilon _{i}}$ is an error term and the subscript ${\displaystyle i}$ indexes a particular ascertainment.

Returning our attending to the straight line instance: Given a random sample from the population, we estimate the population parameters and obtain the sample linear regression model:

${\displaystyle {\widehat {y}}_{i}={\widehat {\beta }}_{0}+{\widehat {\beta }}_{1}x_{i}.}$

The balance, ${\displaystyle e_{i}=y_{i}-{\widehat {y}}_{i}}$ , is the deviation between the value of the dependent variable predicted past the model, ${\displaystyle {\widehat {y}}_{i}}$ , and the true value of the dependent variable, ${\displaystyle y_{i}}$ . One method of interpretation is ordinary least squares. This method obtains parameter estimates that minimize the sum of squared residuals, SSR:

${\displaystyle SSR=\sum _{i=1}^{n}e_{i}^{2}.\,}$

Minimization of this part results in a set of normal equations, a prepare of simultaneous linear equations in the parameters, which are solved to yield the parameter estimators, ${\displaystyle {\widehat {\beta }}_{0},{\widehat {\beta }}_{ane}}$ .

Illustration of linear regression on a data gear up.

In the case of simple regression, the formulas for the to the lowest degree squares estimates are

${\displaystyle {\widehat {\beta }}_{1}={\frac {\sum (x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}{\sum (x_{i}-{\bar {x}})^{2}}}}$

${\displaystyle {\widehat {\beta }}_{0}={\bar {y}}-{\widehat {\beta }}_{one}{\bar {x}}}$

where ${\displaystyle {\bar {x}}}$ is the mean (average) of the ${\displaystyle x}$ values and ${\displaystyle {\bar {y}}}$ is the hateful of the ${\displaystyle y}$ values.

Under the supposition that the population error term has a abiding variance, the estimate of that variance is given by:

${\displaystyle {\hat {\sigma }}_{\varepsilon }^{ii}={\frac {SSR}{n-2}}.\,}$

This is called the mean square error (MSE) of the regression. The denominator is the sample size reduced by the number of model parameters estimated from the same information, ${\displaystyle (n-p)}$ for ${\displaystyle p}$ regressors or ${\displaystyle (n-p-1)}$ if an intercept is used.^[nineteen] In this case, ${\displaystyle p=1}$ so the denominator is ${\displaystyle n-ii}$ .

The standard errors of the parameter estimates are given by

${\displaystyle {\chapeau {\sigma }}_{\beta _{one}}={\chapeau {\sigma }}_{\varepsilon }{\sqrt {\frac {i}{\sum (x_{i}-{\bar {x}})^{ii}}}}}$

${\displaystyle {\hat {\sigma }}_{\beta _{0}}={\lid {\sigma }}_{\varepsilon }{\sqrt {{\frac {one}{n}}+{\frac {{\bar {10}}^{2}}{\sum (x_{i}-{\bar {x}})^{2}}}}}={\hat {\sigma }}_{\beta _{ane}}{\sqrt {\frac {\sum x_{i}^{two}}{northward}}}.}$

Under the further assumption that the population error term is normally distributed, the researcher tin use these estimated standard errors to create confidence intervals and comport hypothesis tests about the population parameters.

General linear model [edit]

In the more full general multiple regression model, there are ${\displaystyle p}$ contained variables:

${\displaystyle y_{i}=\beta _{1}x_{i1}+\beta _{2}x_{i2}+\cdots +\beta _{p}x_{ip}+\varepsilon _{i},\,}$

where ${\displaystyle x_{ij}}$ is the ${\displaystyle i}$ -th observation on the ${\displaystyle j}$ -th independent variable. If the kickoff contained variable takes the value i for all ${\displaystyle i}$ , ${\displaystyle x_{i1}=1}$ , then ${\displaystyle \beta _{i}}$ is called the regression intercept.

The least squares parameter estimates are obtained from ${\displaystyle p}$ normal equations. The residual tin be written as

${\displaystyle \varepsilon _{i}=y_{i}-{\hat {\beta }}_{1}x_{i1}-\cdots -{\hat {\beta }}_{p}x_{ip}.}$

The normal equations are

${\displaystyle \sum _{i=one}^{n}\sum _{thousand=one}^{p}x_{ij}x_{ik}{\lid {\beta }}_{k}=\sum _{i=1}^{n}x_{ij}y_{i},\ j=one,\dots ,p.\,}$

In matrix notation, the normal equations are written as

${\displaystyle \mathbf {(10^{\elevation }10){\chapeau {\boldsymbol {\beta }}}={}10^{\top }Y} ,\,}$

where the ${\displaystyle ij}$ chemical element of ${\displaystyle \mathbf {X} }$ is ${\displaystyle x_{ij}}$ , the ${\displaystyle i}$ element of the column vector ${\displaystyle Y}$ is ${\displaystyle y_{i}}$ , and the ${\displaystyle j}$ element of ${\displaystyle {\hat {\boldsymbol {\beta }}}}$ is ${\displaystyle {\hat {\beta }}_{j}}$ . Thus ${\displaystyle \mathbf {10} }$ is ${\displaystyle due north\times p}$ , ${\displaystyle Y}$ is ${\displaystyle due north\times one}$ , and ${\displaystyle {\hat {\boldsymbol {\beta }}}}$ is ${\displaystyle p\times 1}$ . The solution is

${\displaystyle \mathbf {{\chapeau {\boldsymbol {\beta }}}=(X^{\summit }X)^{-i}X^{\top }Y} .\,}$

Diagnostics [edit]

Once a regression model has been constructed, it may be important to ostend the goodness of fit of the model and the statistical significance of the estimated parameters. Normally used checks of goodness of fit include the R-squared, analyses of the pattern of residuals and hypothesis testing. Statistical significance can be checked by an F-exam of the overall fit, followed past t-tests of individual parameters.

Interpretations of these diagnostic tests rest heavily on the model's assumptions. Although exam of the residuals can be used to invalidate a model, the results of a t-test or F-test are sometimes more difficult to interpret if the model's assumptions are violated. For example, if the error term does not take a normal distribution, in modest samples the estimated parameters will not follow normal distributions and complicate inference. With relatively large samples, however, a central limit theorem can exist invoked such that hypothesis testing may go on using asymptotic approximations.

Limited dependent variables [edit]

Express dependent variables, which are response variables that are chiselled variables or are variables constrained to autumn but in a sure range, often ascend in econometrics.

The response variable may exist not-continuous ("express" to lie on some subset of the real line). For binary (null or one) variables, if analysis gain with least-squares linear regression, the model is called the linear probability model. Nonlinear models for binary dependent variables include the probit and logit model. The multivariate probit model is a standard method of estimating a joint relationship between several binary dependent variables and some independent variables. For categorical variables with more than two values there is the multinomial logit. For ordinal variables with more than than 2 values, there are the ordered logit and ordered probit models. Censored regression models may be used when the dependent variable is only sometimes observed, and Heckman correction type models may be used when the sample is not randomly selected from the population of interest. An alternative to such procedures is linear regression based on polychoric correlation (or polyserial correlations) between the categorical variables. Such procedures differ in the assumptions made about the distribution of the variables in the population. If the variable is positive with low values and represents the repetition of the occurrence of an issue, so count models like the Poisson regression or the negative binomial model may exist used.

Nonlinear regression [edit]

When the model role is not linear in the parameters, the sum of squares must be minimized by an iterative procedure. This introduces many complications which are summarized in Differences betwixt linear and non-linear least squares.

Interpolation and extrapolation [edit]

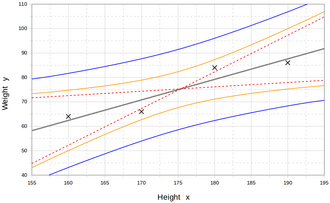
In the middle, the interpolated directly line represents the best balance betwixt the points above and below this line. The dotted lines stand for the two farthermost lines. The starting time curves represent the estimated values. The outer curves represent a prediction for a new measurement.^[20]

Regression models predict a value of the Y variable given known values of the X variables. Prediction within the range of values in the dataset used for model-fitting is known informally as interpolation. Prediction outside this range of the data is known as extrapolation. Performing extrapolation relies strongly on the regression assumptions. The further the extrapolation goes outside the data, the more room there is for the model to fail due to differences between the assumptions and the sample data or the true values.

It is by and large advised^{[ citation needed ]} that when performing extrapolation, one should accompany the estimated value of the dependent variable with a prediction interval that represents the uncertainty. Such intervals tend to expand chop-chop equally the values of the contained variable(southward) moved outside the range covered by the observed information.

For such reasons and others, some tend to say that information technology might be unwise to undertake extrapolation.^[21]

Even so, this does not cover the full set of modeling errors that may exist made: in particular, the assumption of a detail form for the relation between Y and Ten. A properly conducted regression analysis volition include an assessment of how well the causeless form is matched by the observed data, but information technology tin only do and then within the range of values of the independent variables actually bachelor. This means that any extrapolation is peculiarly reliant on the assumptions being made almost the structural course of the regression human relationship. Best-do communication here^{[ citation needed ]} is that a linear-in-variables and linear-in-parameters relationship should non be chosen but for computational convenience, just that all available knowledge should be deployed in amalgam a regression model. If this knowledge includes the fact that the dependent variable cannot become outside a sure range of values, this can be made use of in selecting the model – even if the observed dataset has no values particularly about such premises. The implications of this stride of choosing an appropriate functional form for the regression can be corking when extrapolation is considered. At a minimum, it tin can ensure that any extrapolation arising from a fitted model is "realistic" (or in accord with what is known).

Power and sample size calculations [edit]

At that place are no generally agreed methods for relating the number of observations versus the number of contained variables in the model. I method conjectured by Proficient and Hardin is ${\displaystyle Due north=m^{n}}$ , where ${\displaystyle North}$ is the sample size, ${\displaystyle n}$ is the number of independent variables and ${\displaystyle yard}$ is the number of observations needed to attain the desired precision if the model had only one independent variable.^[22] For example, a researcher is building a linear regression model using a dataset that contains chiliad patients ( ${\displaystyle N}$ ). If the researcher decides that five observations are needed to precisely define a straight line ( ${\displaystyle m}$ ), then the maximum number of contained variables the model tin back up is 4, because

${\displaystyle {\frac {\log 1000}{\log 5}}=4.29.}$

Other methods [edit]

Although the parameters of a regression model are normally estimated using the method of least squares, other methods which have been used include:

• Bayesian methods, e.g. Bayesian linear regression
• Percentage regression, for situations where reducing per centum errors is accounted more appropriate.^[23]
• Least absolute deviations, which is more than robust in the presence of outliers, leading to quantile regression
• Nonparametric regression, requires a large number of observations and is computationally intensive
• Scenario optimization, leading to interval predictor models
• Altitude metric learning, which is learned by the search of a meaningful distance metric in a given input space.^[24]

Software [edit]

All major statistical software packages perform least squares regression assay and inference. Simple linear regression and multiple regression using to the lowest degree squares can be washed in some spreadsheet applications and on some calculators. While many statistical software packages can perform various types of nonparametric and robust regression, these methods are less standardized. Different software packages implement different methods, and a method with a given name may be implemented differently in different packages. Specialized regression software has been developed for apply in fields such every bit survey analysis and neuroimaging.

See also [edit]

• Anscombe's quartet
• Bend plumbing equipment
• Estimation theory
• Forecasting
• Fraction of variance unexplained
• Part approximation
• Generalized linear models
• Kriging (a linear least squares interpretation algorithm)
• Local regression
• Modifiable areal unit problem
• Multivariate adaptive regression splines
• Multivariate normal distribution
• Pearson production-moment correlation coefficient
• Quasi-variance
• Prediction interval
• Regression validation
• Robust regression
• Segmented regression
• Signal processing
• Stepwise regression
• Taxicab geometry
• Trend estimation

References [edit]

1. ^ Necessary Condition Analysis
2. ^ David A. Freedman (27 Apr 2009). Statistical Models: Theory and Practise. Cambridge University Printing. ISBN978-1-139-47731-4.
3. ^ R. Dennis Cook; Sanford Weisberg Criticism and Influence Analysis in Regression, Sociological Methodology, Vol. 13. (1982), pp. 313–361
4. ^ A.M. Legendre. Nouvelles méthodes pour la détermination des orbites des comètes, Firmin Didot, Paris, 1805. "Sur la Méthode des moindres quarrés" appears as an appendix.
5. ^ ^{a b} Chapter 1 of: Angrist, J. D., & Pischke, J. S. (2008). Mostly Harmless Econometrics: An Empiricist's Companion. Princeton University Press.
6. ^ C.F. Gauss. Theoria combinationis observationum erroribus minimis obnoxiae. (1821/1823)
7. ^ Mogull, Robert G. (2004). Second-Semester Practical Statistics. Kendall/Chase Publishing Company. p. 59. ISBN978-0-7575-1181-iii.
8. ^ Galton, Francis (1989). "Kinship and Correlation (reprinted 1989)". Statistical Science. 4 (2): fourscore–86. doi:x.1214/ss/1177012581. JSTOR 2245330.
9. ^ Francis Galton. "Typical laws of heredity", Nature 15 (1877), 492–495, 512–514, 532–533. (Galton uses the term "reversion" in this paper, which discusses the size of peas.)
10. ^ Francis Galton. Presidential address, Section H, Anthropology. (1885) (Galton uses the term "regression" in this paper, which discusses the top of humans.)
11. ^ Yule, G. Udny (1897). "On the Theory of Correlation". Journal of the Regal Statistical Society. threescore (iv): 812–54. doi:10.2307/2979746. JSTOR 2979746.
12. ^ Pearson, Karl; Yule, One thousand.U.; Blanchard, Norman; Lee,Alice (1903). "The Constabulary of Bequeathed Heredity". Biometrika. ii (two): 211–236. doi:10.1093/biomet/2.2.211. JSTOR 2331683.
13. ^ Fisher, R.A. (1922). "The goodness of fit of regression formulae, and the distribution of regression coefficients". Journal of the Purple Statistical Gild. 85 (4): 597–612. doi:10.2307/2341124. JSTOR 2341124. PMC1084801.
14. ^ Ronald A. Fisher (1954). Statistical Methods for Research Workers (12th ed.). Edinburgh: Oliver and Boyd. ISBN978-0-05-002170-5.
15. ^ Aldrich, John (2005). "Fisher and Regression". Statistical Science. twenty (4): 401–417. doi:ten.1214/088342305000000331. JSTOR 20061201.
16. ^ Rodney Ramcharan. Regressions: Why Are Economists Obessessed with Them? March 2006. Accessed 2011-12-03.
17. ^ Fotheringham, A. Stewart; Brunsdon, Chris; Charlton, Martin (2002). Geographically weighted regression: the assay of spatially varying relationships (Reprint ed.). Chichester, England: John Wiley. ISBN978-0-471-49616-8.
18. ^ Fotheringham, AS; Wong, DWS (1 January 1991). "The modifiable areal unit problem in multivariate statistical assay". Environs and Planning A. 23 (7): 1025–1044. doi:10.1068/a231025. S2CID 153979055.
19. ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Loma, 1960, page 288.
20. ^ Rouaud, Mathieu (2013). Probability, Statistics and Estimation (PDF). p. 60.
21. ^ Chiang, C.Fifty, (2003) Statistical methods of analysis, Earth Scientific. ISBN 981-238-310-7 - page 274 department 9.7.4 "interpolation vs extrapolation"
22. ^ Good, P. I.; Hardin, J. W. (2009). Common Errors in Statistics (And How to Avoid Them) (3rd ed.). Hoboken, New Bailiwick of jersey: Wiley. p. 211. ISBN978-0-470-45798-half dozen.
23. ^ Tofallis, C. (2009). "Least Squares Percentage Regression". Journal of Modern Applied Statistical Methods. seven: 526–534. doi:x.2139/ssrn.1406472. SSRN 1406472.
24. ^ YangJing Long (2009). "Human age estimation past metric learning for regression problems" (PDF). Proc. International Briefing on Figurer Analysis of Images and Patterns: 74–82. Archived from the original (PDF) on 2010-01-08.

Further reading [edit]

• William H. Kruskal and Judith M. Tanur, ed. (1978), "Linear Hypotheses," International Encyclopedia of Statistics. Complimentary Press, five. 1,

Evan J. Williams, "I. Regression," pp. 523–41.

Julian C. Stanley, "II. Assay of Variance," pp. 541–554.

• Lindley, D.V. (1987). "Regression and correlation analysis," New Palgrave: A Dictionary of Economics, v. 4, pp. 120–23.
• Birkes, David and Dodge, Y., Alternative Methods of Regression. ISBN 0-471-56881-three
• Chatfield, C. (1993) "Calculating Interval Forecasts," Periodical of Business organisation and Economical Statistics, xi. pp. 121–135.
• Draper, N.R.; Smith, H. (1998). Applied Regression Assay (3rd ed.). John Wiley. ISBN978-0-471-17082-2.
• Fox, J. (1997). Applied Regression Analysis, Linear Models and Related Methods. Sage
• Hardle, Westward., Practical Nonparametric Regression (1990), ISBN 0-521-42950-one
• Meade, Nigel; Islam, Towhidul (1995). "Prediction intervals for growth curve forecasts". Periodical of Forecasting. 14 (5): 413–430. doi:10.1002/for.3980140502.
• A. Sen, Thou. Srivastava, Regression Assay — Theory, Methods, and Applications, Springer-Verlag, Berlin, 2011 (4th printing).
• T. Strutz: Data Fitting and Uncertainty (A applied introduction to weighted least squares and across). Vieweg+Teubner, ISBN 978-three-8348-1022-ix.
• Stulp, Freek, and Olivier Sigaud. Many Regression Algorithms, One Unified Model: A Review. Neural Networks, vol. 69, Sept. 2015, pp. 60–79. https://doi.org/10.1016/j.neunet.2015.05.005.
• Malakooti, B. (2013). Operations and Product Systems with Multiple Objectives. John Wiley & Sons.

External links [edit]

• "Regression analysis", Encyclopedia of Mathematics, Ems Press, 2001 [1994]
• Earliest Uses: Regression – basic history and references
• What is multiple regression used for? – Multiple regression
• Regression of Weakly Correlated Information – how linear regression mistakes tin can appear when Y-range is much smaller than X-range
• Polynomial Regression – How y'all tin can tweak information in order to run non-linear regression analysis

Can Regression Analysis Be Used A Data That The Distribution Is Skewed?,

Source: https://en.wikipedia.org/wiki/Regression_analysis

Posted by: griffithabore1949.blogspot.com

Share this post